椭圆方程椭圆的两个焦点在y轴上时,怎么推导方程式
解:设椭圆上焦点F&拭貉强跳#8321;(0,c),下焦点F₂(0,-c);c为半焦距,c>0。
椭圆上的动点M(x,y);依椭圆定义有等式:
∣MF₁∣+∣MF₂∣=√[x²+(y-c)²]+√[x²+(y+c)²]=2a,a为长半轴之长,a>0。
√[x²+(y-c)²]=2a-√[x²+(y+c)²]
两边平方得:x²+(y-c)²=4a²-4a√[x²+(y+c)²]+x²+(y+c)²化简、移项,得4a√[x²(y+c)²]=4a²+4c
化小系数得:a√[x²+(y+c)²]=a²+cy
再平方得:a²[x²+(y+c)²]=a^4+2a²cy+c²y²
a²x²+(a²-c²)y²=a^4-a²c²
令a²-c²=b²,得a²x²+b²y²=a²b²
再用a²b²除两边,即得焦点在y轴上的椭圆的标准方程为:
y²/a²+x²/b²=1,其中a²-b²=c²;a>b.
其中a为长半轴之长,b为短半轴之长,c为半焦距。
扩展资料:
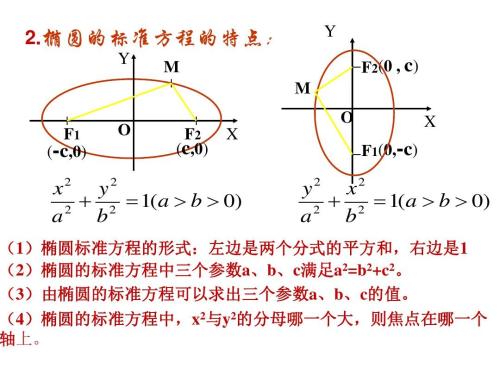
椭圆方程的几何性质
X,Y的范围
当焦点在X轴时 -a≤x≤a,-b≤y≤b
当焦点在Y轴时 -b≤x≤b,-a≤y≤a
对称性
不论焦点在X轴还是Y轴,椭圆始终关于X/Y/原点对称。
顶点:
焦点在X轴时:长轴顶点:(-a,0),(a,0)
短轴顶点:(0,b),(0,-b)
焦点在Y轴时:长轴顶点:(0,-a),(0,a)
短轴顶点:(b,0),(-b,0)
注意长短轴分别代表哪一条轴,在此容易引起混乱,还需数形结合逐步理解透彻。
焦点:
当焦点在X轴上时焦点坐标F1(-c,0)F2(c,0)
当焦点在Y轴上时焦点坐标F1(0,-c)F2(0,c)
计算方法
编辑
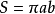
((其中
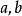
分别是椭圆的长半轴、短半轴的长,可由圆的面积可推导出来)或
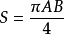
(其中
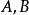
分别是椭圆的长轴,短轴的长)。
圆和椭圆之间的关系:
椭圆包括圆,圆是特殊的椭圆。
参考资料来源:百度百科--椭圆参数方程